| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 알고리즘
- JavaScript
- JS
- 엔퀸즈
- 일상
- Instantiation Patterns
- method
- 공부
- underscores
- DOM
- this
- 제일어려워
- ftech
- react
- 초보
- 개발
- 연습
- 해커톤
- vscode
- underbar
- array
- 포스기
- 자바스크립트
- nqueens
- 클라이언트
- 취업
- 리액트
- 코딩
- 코드스테이츠
- grpahQL
- Today
- Total
analogcoding
Data structure - part.2 본문
Graph 구조
모든 노드를 각각 노드와 연결하는 선을 하나로 모아 놓은 비선형(non-linear) 자료구조로 노드(node)와 엣지(edge)로 구성되어있다.
Graph 종류
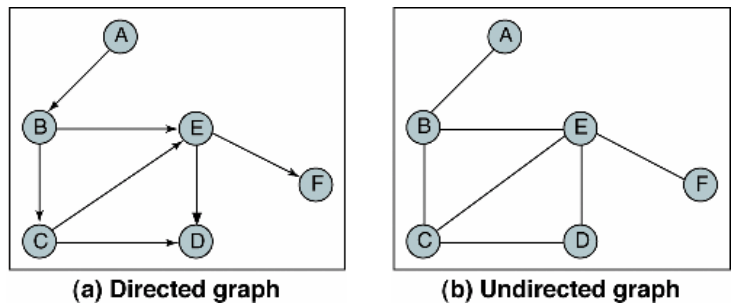
1) 방향 그래프(directed) 정점 간의 간선 방향이 존재할 경우
2) 무방향 그래프(undirected) 정점 간의 간선 방향이 없을 경우
3) 가중치 그래프(weighted or Network) 정점 간의 간선이 특정 값을 가지는 경우
그래프는 방향에 구애를 딱히 받지 않는다.
그래프에는 사이클이 존재 할 수도 있고 없을 수도 있다.
Root Node 의 개념이 없다. ( 부모,자식 개념이 없다 )
그래프의 구현
1. 인접리스트(Adjacency list)
ㄴ 접근이 빠르지만 메모리의 낭비가 심함.
2. 인접행렬(Adjacency matrix, 2차 행렬)
ㄴ 접근이 느린 대신, 메모리의 낭비가 적음.
그래프 검색(탐색) 방법
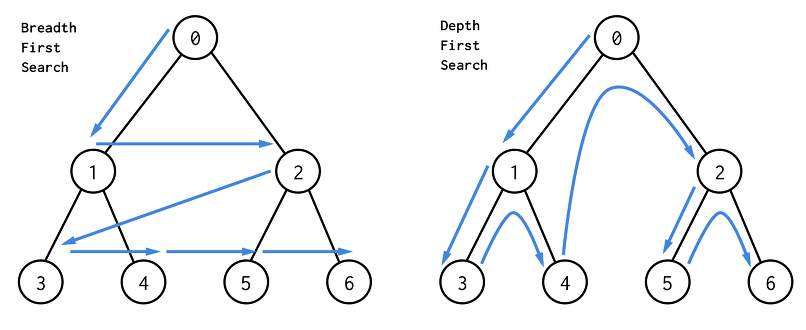
DFS, Depth First Search (깊이우선검색)
트리구조 순회방법과 같이 Root Node 혹은 다른 Node에서 시작해서 child Node가 끝날때까지 child Node를 검색하고,
childe Node가 끝나면, 위로 올라가 sbling Node를 동일한 방법으로 검색하는 방법이다.
0 1 3 4 2 5 6 순
즉 최대한 깊숙히 탐색한 후 다시 돌아가 다른 루트를 탐색한다. 여기서 한 노드에서 제일 마지막 자식까지 탐색을 마치고 돌아오는
과정을 백트리킹(Backtracking)이라고 하고 구현에는 주로 스택 자료구조를 사용.
BFS, Breath First Search (넓이우선검색)
트리 혹은 그래프에서 노드의 인접한 모든 정점들을 우선으로 탐색하는 방법으로 Root Node 혹은 다른 Node에서 시작해서
Child Node를 먼저 검색하고, 검색이 끝나면 Child Node의 동일선의 Node를 검색하는 방법으로 넓게 검색한다.
0 1 2 3 4 5 6 순
출발 노드에서 목표 노드까지의 최단 길이 경로를 보장하는 방법이다. 구현에는 주로 큐 자료구조를 사용.
수도코드
DFS
1. 데이터를 담을 스택 생성
2. 최상단 위치한 노드(root)를 하나씩 차례대로 스택에 삽입한다.
3. 단, 한 반복에 스택의 top이 하나씩 계속 출력되도록 한다.
4. 만약, 출력된 노드에 자식노드가 있다면, 스택에 담아주도록 한다.
5. 자식노드가 없다면 스택에 담지 않고 출력한다.
BFS
1. 데이터를 담을 큐를 생성
2. 큐에 최상단 노드(root)부터 하나씩 큐에 삽입한다.
3. dequeque된 노드의 데이터를 출력해주고, 출력된 노드에 자식노드가 있다면 차례대로 큐에 넣어준다. ==>1번
4. 출력된 노드에 자식노드가 없다면, 출력만 해준다.
Tree 구조
+ B-Tree
B-트리(B-tree)는 데이터베이스와 파일 시스템에서 널리 사용되는 트리구조의 일종으로, 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조이다.
방대한 양의 저장된 자료를 검색해야 하는 경우 검색어와 자료를 일일이 비교하는 방식은 비효율적이다. B-트리는 자료를 정렬된 상태로 보관하고, 삽입 및 삭제를 대수 시간으로 할 수 있다. 대부분의 이진트리는 항목이 삽입될 때 하향식으로 구성되는 데 반해, B-트리는 일반적으로 상향식으로 구성된다.
용어
-
루트(Root)
-
트리는 노드(node)들과 노드들을 연결하는 링크(link)들로 구성된다.
-
맨 위의 노드를 루트라고 한다.
-
-
부모-자식(parent-child) 관계
-
각 노드들의 상하 관계를 부모-자식(parent-child)관계로 나타낸다.
-
-
형제 관계(sibling)
-
루트노드를 제외한 트리의 모든 노드들은 유일한 부모노드를 가진다.
-
부모가 동일한 노드들을 형제 관계라고 부른다.
-
-
리프(leaf) 노드
-
자식이 없는 노드들을 leaf노드라고 부른다.
-
리프노드가 아닌 노드들을 내부(internal)노드라고 부른다.
-
-
조상-자손(ancestor-descendant) 관계
-
부모-자식 관계를 확장한 것이 조상-자손 관계이다.
-
-
subtree
-
트리의 특성상 한 노드의 자손노드들의 집합도 트리이다.
-
트리에서 어떤 한 노드와 그 노드의 자손들로 이루어진 트리를 subtree라고 부른다.
-
-
레벨(level)
-
root노드는 level 1
-
root노드의 자식노드들은 level 2
-
-
높이
-
서로다른 레벨의 수이다.
-
특징
1. 1개의 Root Node를 가진다.
2. Root Node 는 0개 이상의 Child Node 를 갖는다.
3. Child Node 또한 0개 이상의 Child Node 를 가지고 이는 반복적으로 정의된다.
4. Cycle 이 존재 할 수 없다.
5. 부모 Node 와 연결이 있을 수도, 없을 수도 있다.
6.루트에서 어떤 노드로 가는 경로는 유일하다.
임의의 두 노드 간의 경로도 유일하다. 즉, 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
종류
1. 이진 트리(binary tree)
각 Node가 최대 2개의 Child Node를 갖는 트리를 말한다. 사실 모든 트리가 이진트리는 아니다.
자식을 3개 가지면 삼진(ternary tree)라고 부른다.
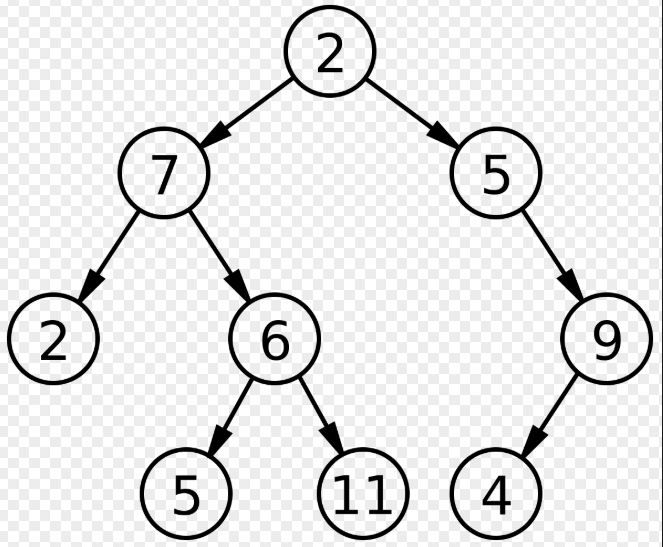
탐색방법.
1. InOrder
2. PreOrder
3. PostOrder
수도코드
노드를 생설할 생성자함수 생성
객체생성 (data)
this.value = data ,
this.leftChild = null,
this.rightChild = null 을 가짐
노드삽입함수 생성
leftChild
rightChild
노드탐색함수 생성
인자로 찾을 taget를 주어서 this.value 와 일치하지 않으면
this.value.rightChild 와
this.value.leftChild 를 일치하는지 검사하고 맞다면 리턴
아니라면 재귀적으로 계속 다시 넣어준다.
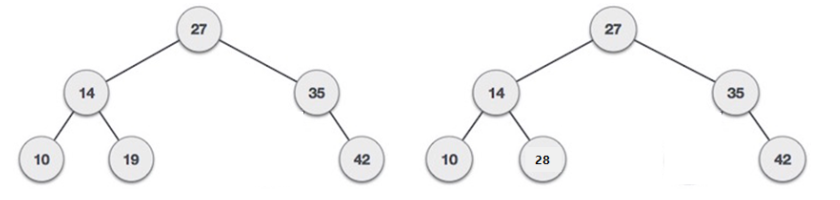
2. 이진탐색트리(binary search tree)
이진트리와는 다르게 특정 조건을 만족해야한다.
( 모든 왼쪽 Child Node <= 현재 Node < 모든 오른쪽 Child Node )
수도코드
data (val) 를 인자로 받는 함수 binerysearchtree 함수 생성
this.value = val
this.left = null
this.right = null
프로토타입을 만들고 insert 메소드를 생성 (인자로)
binerysearchtree.prototype.insert = function(val){
조건 생성
인자로 받은 val 가 this.value 와 this.left 보다 작을 때
left노드에 추가 this.left.insert(val)
인자로 받은 val 가 this.value 보다 크면서 this.left 보다 작지 않을 때
left노드에 new 생성자 함수에 인자를 넣어서 다시 재귀실행.
인자로 받은 val 가 this.value 와 this.right 보다 클 때
right노드에 추가 this.right.insert(val)
인자로 받은 val 가 this.value 보다 크면서 this.left 보다 크지 않을 때
right노드에 new 생성자 함수에 인자를 넣어서 다시 재귀실행.
3. 완전이진트리(complete binary tree)
트리의 모든 높이(또는 깊이) 에서 Node가 꽉 차있는 이진트리를 말한다.
완전 이진 트리는 왼쪽자식노드부터 채워지며 마지막 레벨을 제외하고는 모든 자식노드가 채워져있는 트리이다.
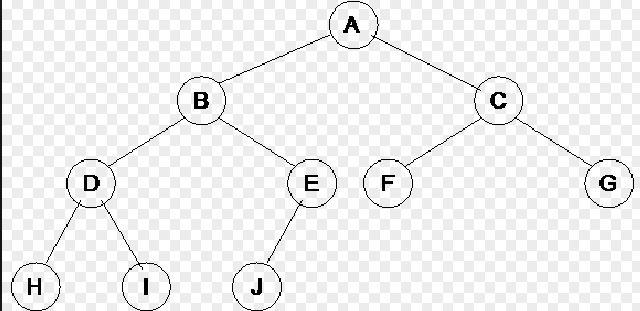
4. 포화 이진 트리(perfect binary tree)
포화 이진 트리는 모든 노드가 0개 혹은 2개의 자식노드를 가지며 모든 리프노드가 똑같은 레벨에 있는 경우의 트리이다.
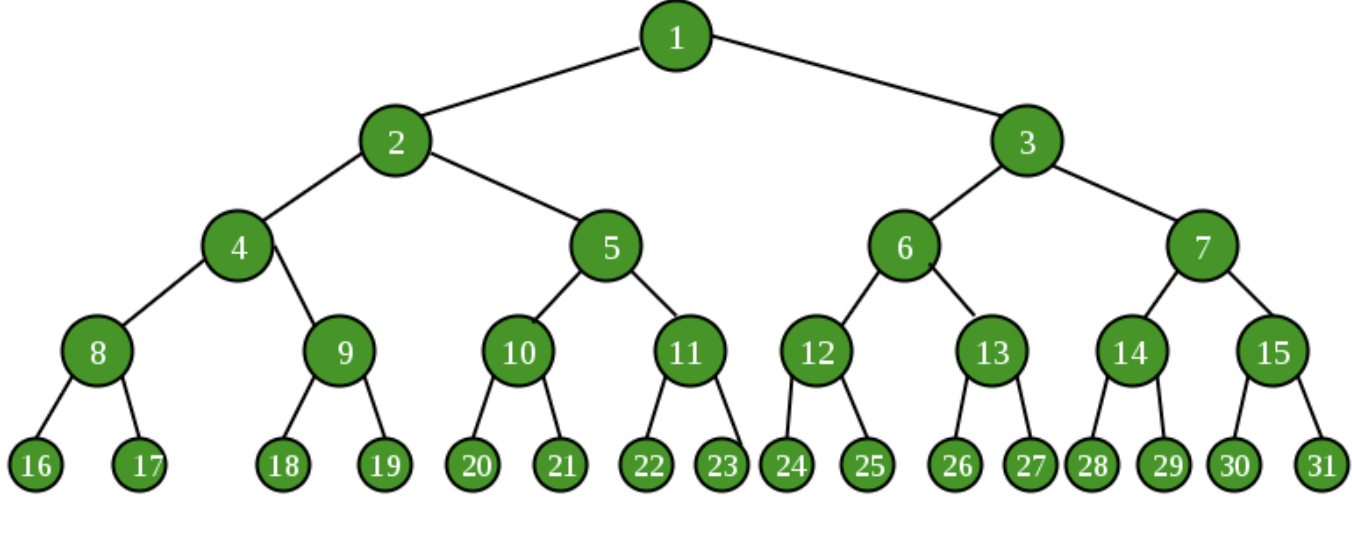
5. 전 이진트리(full binary tree)
모든 Node의 Child Node가 없거나 정확히 두개 있는 경우를 말함.

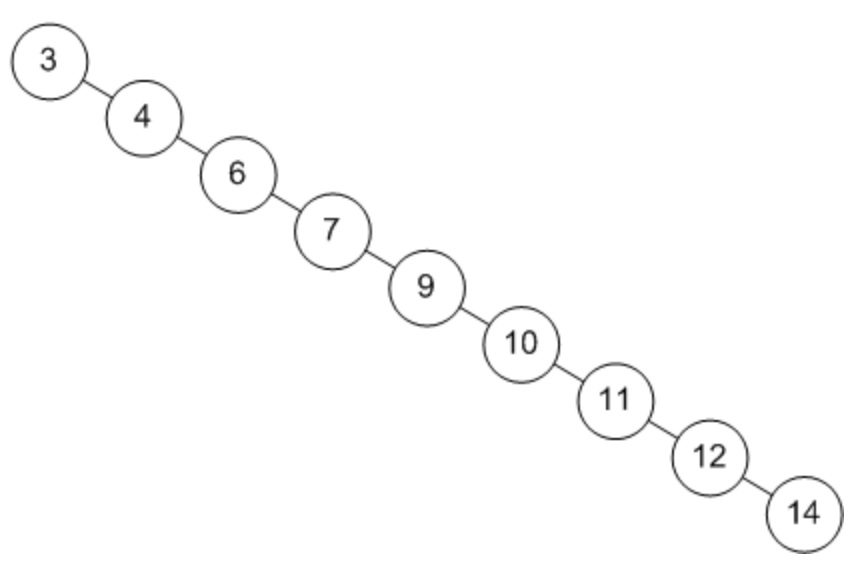
6. 편향 이진 트리(skewed binary tree)
편향 이진 트리는 말 그대로 노드들이 전부 한 방향으로 편향된 트리이다.
Hash table
해시함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 색인(key) 혹은 주소 삼아 데이터의 값(value)을 키와 함께 저장하는 자료구조를 해시테이블(hash table)이라고 한다.
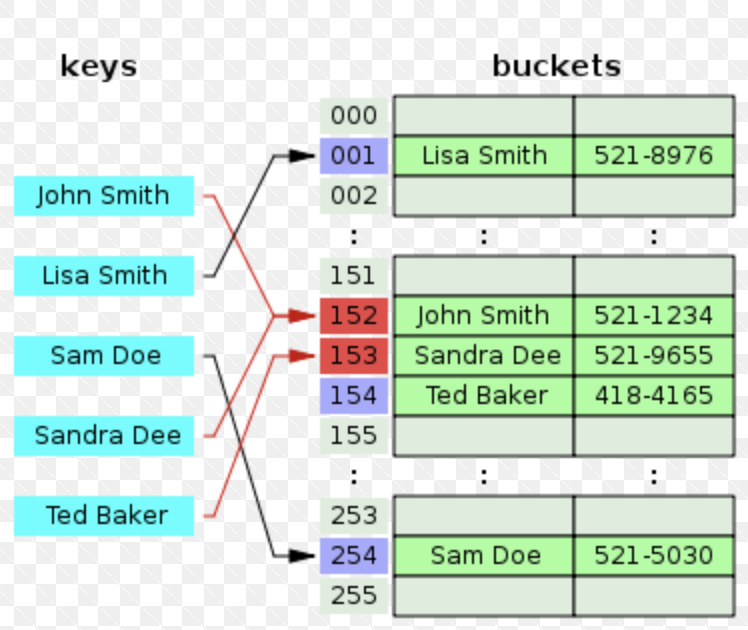
그런데 데이터의 양이 방대해지면 해시 알고리즘에서 key 값 중복이 일어나는데 이 것을 충돌(collision)이라 한다.
충돌 해결
1. Separate chaining 방식
만약에 key 중복으로 인해서 충돌이 발생하면 그 key가 가리키고 있는 Linked list에 노드를 추가하여 값을 추가한다.
2. Open addressing 방식
Linked List와 같은 추가적인 메모리 공간을 사용하지 않고, hash table array의 빈공간에 채워넣는 사용하는 방법으로,
Separate chaining 방식에 비해서 메모리를 덜 사용한다.
해쉬 함수란?
해시함수(hash function)란 데이터의 효율적 관리를 목적으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수.
수도코드
고정된 배열을 선언
노드를 생성
해시 함수를 거침
키를 받아서 만든 해시코드를 버켓에 배치
충돌을 방지하기 위해 같은 인덱스 내에 여러개의 데이터가 들어온다면 내부에 이중배열을 생성하거나 Linked list를 생성.
정말 구조가 이해가 안 가고 아직 머릿 속에 그려지지 않음.....
'Be well coding > Learn more' 카테고리의 다른 글
| N-Queens (0) | 2019.06.10 |
|---|---|
| Interact with Server - what is Web Architecture (0) | 2019.06.08 |
| Object.create() & Class & Super Method (0) | 2019.06.03 |
| Inheritance Patterns (0) | 2019.06.03 |
| Data structure - part.1 (0) | 2019.05.29 |



